A Comprehensive Guide to Ratchet and Pawl System Theory: Mechanics, Thermodynamics, and Applications

The ratchet and pawl system is far more than just a simple mechanical device—it stands at the intersection of engineering, physics, and even philosophy. It’s a ubiquitous tool in everyday objects and a profound example in fundamental scientific inquiry. While to some it might simply be the mechanism behind a socket wrench or a water well, deeper exploration reveals it as a cornerstone in our understanding of motion, energy, and the arrow of time.

Across centuries, the humble ratchet and pawl has been reimagined in everything from industrial machines to thought experiments on the limits of physics. This mechanism unlocks both practical advantages, like enabling controlled movement or lifting heavy loads with ease, and deep theoretical insights about the universe, such as why perpetual motion is impossible and why time only seems to move forward. Let’s dive into the details of how this mechanism works, its many forms, and its profound significance across science and technology.

Understanding the Basics: What Is a Ratchet and Pawl System?

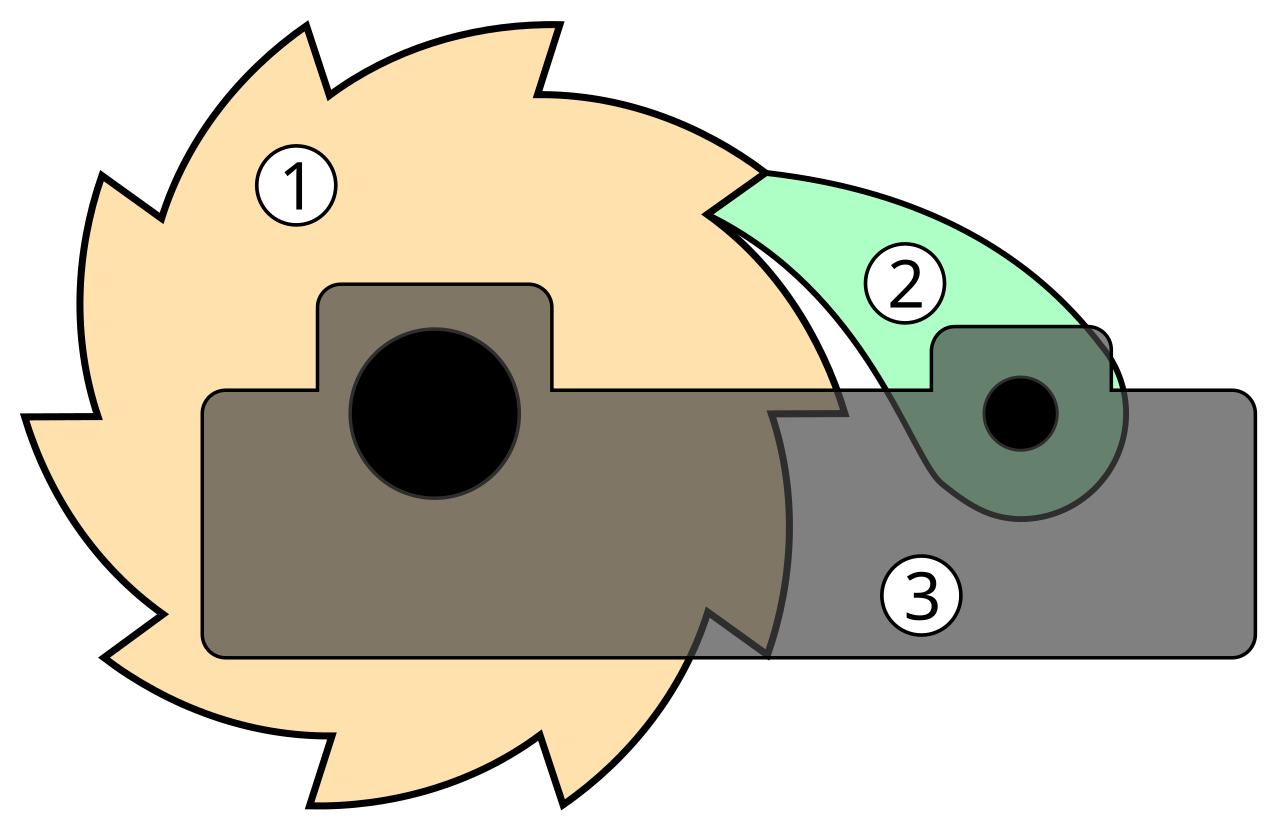
At its core, the ratchet and pawl mechanism allows motion in one direction and prevents movement in the other. It typically consists of a toothed wheel—the ratchet—and a spring-loaded lever or finger called the pawl. As the wheel turns, the pawl slides over the gently sloping teeth, clicking into the gaps. If the wheel tries to turn the other way, the pawl locks against the steep edge of a tooth, blocking backward motion.

This clever design is the reason tools like socket wrenches can tighten bolts with rapid, repetitive action while never loosening them. Similarly, it explains why a well bucket doesn’t unwind uncontrollably: the pawl ‘catches’ the weight, locking it in place when you release the handle.

The key features of a basic ratchet and pawl system are:

• Ratchet Wheel or Gear: A circular gear (or sometimes a linear rack) with asymmetrical teeth. One side of each tooth has a gradual slope, while the other is much steeper.
• Pawl: A pivoting lever or latch—usually attached with a spring—that engages with the teeth so it can slip over them in one direction and lock against them in the other.
• Spring Mechanism: Keeps the pawl pressed into the gear, ensuring firm engagement and reliable operation.

Whenever the system is engaged, it allows stepwise rotation—typically in only one direction—providing both control and safety. This makes it indispensable in countless everyday devices and complex machinery alike.

The Mechanics of the Ratchet and Pawl: How It Really Works

The action of the ratchet and pawl is straightforward in appearance, but the details matter greatly. The way the pawl drops into the teeth, the angle and shape of the teeth, and the spring tension all work together to create a reliable one-way mechanism.

When the ratchet wheel rotates in the ‘allowed’ direction, the sloped edges of the teeth guide the pawl up and over, with the spring pushing it downward so it drops into each gap. You might even hear those satisfying clicks in a ratchet wrench or a turning winch. As soon as you try to reverse, the pawl jams against the steep edge of the nearest tooth, stopping backward motion instantly.

However, ratchets are not perfect ‘locks’—there’s always a tiny amount of backward movement possible, known as ‘backlash.’ This is the arc through which the wheel can move before the pawl hits the next tooth. In high-precision situations, such as in specialist machinery or scientific instruments, designers sometimes use toothless ratchets with high-friction surfaces. Here, the pawl jams against a rubbery, angled surface, reducing backlash to almost nothing.

Key points about the physical interaction:

• The shape and pitch of the teeth dictate how smoothly the mechanism moves and how much backward movement is possible before locking.
• The strength of the spring and the placement of the pawl determine how firmly the system engages, influencing both reliability and wear.
• Multiple pawls can be used for extra security or to minimize backlash, staggered so that as one disengages, another is ready to catch.

Designers often refine the contact angle between the pawl and the tooth—as the underlying physics determines whether the pawl stays locked or gets forced out under heavy load. Ideally, the common normal (a line perpendicular to the contact point) should pass between the centers of the ratchet and the pawl, ensuring force pulls the pawl deeper into engagement rather than ejecting it.

Classic Applications: Where Are Ratchets and Pawls Used?

This quintessential mechanism appears in more places than you might think. Here’s a quick rundown of just a few everyday and specialized applications:

• Hand Tools: Socket wrenches, caulking guns, and grease guns all rely on ratchets for controlled, one-way operation.
• Lifting Devices: Jacks, winches, and cranes use ratchets to prevent loads from slipping, giving operators the ability to pause safely during lifting.
• Clocks & Watches: The familiar ‘tick-tock’ of winding comes courtesy of a ratchet, which keeps the mainspring from unwinding.
• Vehicles: Bicycles use freewheel mechanisms—essentially a ratchet that lets the rear wheel spin freely when you stop pedaling yet locks to drive the bike forward when you pedal again.
• Safety Systems: Seatbelts, anti-rollback devices in roller coasters, and even handcuffs put ratchet and pawl mechanisms to good use for protection and security.
• Everyday Fasteners: Cable ties and tie-down straps use a simple ratchet to secure loads tightly, only releasing when specifically disengaged.

Even keyboards, looms, turnstiles, and typewriters exploit this principle to control motion, counting, or locking within their intricate mechanisms. The prevalence of the system is a testament to its effectiveness—and adaptability across scales and industries.

Variants and Relatives: Overrunning Clutches, Intermittent Gears, and Beyond

The ratchet and pawl has inspired a family of related mechanisms, all using the basic principle of ‘one-way’ motion. Here are some of the most notable variants:

Overrunning Clutch (Freewheel Mechanism)

An overrunning clutch is a specialized ratchet where the locking and releasing is done via rollers or balls instead of a classic pawl. As the driver delivers torque in the designated direction, the rollers wedge into tapered recesses, providing a secure drive. If the load tries to drive the system in reverse, the rollers become free, and no torque is transmitted—the device ‘overruns,’ letting the driven part spin independently.

Bicycle rear axles are the classic example, enabling coasting while still locking up as soon as you pedal forward. You’ll also find them in automatic transmissions and various industrial machines where unidirectional or free-wheeling motion is needed.

Intermittent Gearing

Intermittent gearing takes the idea a step further by combining continuous driver rotation with alternating motion in the follower. Think of old-school motion picture machines or counting mechanisms. The ‘Geneva Wheel’ is a famous arrangement where a pin on the driver intermittently engages a slot on the follower, causing it to move in discrete steps. Between these impulses, the driven wheel remains locked in place—again, thanks to clever ratchet-like teeth or locking surfaces.

Counting mechanisms, mechanical clocks, and even feed mechanisms in machine tools often use forms of intermittent gearing for precise control over stepwise operations.

Geneva Wheel and Its Unique Action

The Geneva wheel stands out as a classic intermittent gear system. In its typical configuration, each full turn of the driver wheel advances the driven wheel by a fixed fraction—often a quarter turn. When not engaged by the pin, circular sections of the driver mesh with the follower’s rim, securely locking it in place and preventing accidental movement.

This design became widely known as the ‘Geneva stop’ after being used in watches and music boxes to prevent overwinding. Its precision and reliability have kept it relevant from classic horology to modern industrial automation.

Universal Joints and Compound Mechanisms

While not themselves ratcheting devices, universal joints illustrate how multiple motion-control mechanisms are often combined. These joints connect shafts at angles in automotive driveshafts or machinery, allowing torque to be transmitted despite misalignment. When paired with ratchets, they can transmit controlled, stepwise motion across otherwise awkward geometries.

Delving Deeper: The Ratchet and Pawl in Thermodynamics and Statistical Mechanics

Surprisingly, the humble ratchet and pawl sits at the heart of some of physics’ most profound questions. The device has been central to debates about perpetual motion, entropy, and the very direction of time.

The Brownian Ratchet: Feynman’s Famous Thought Experiment

Physicist Richard Feynman famously analyzed the ratchet and pawl in the context of thermal motion—Brownian motion—to explore whether it could produce work purely from random molecular kicks. Imagine a tiny ratchet and pawl setup, connected to a paddle wheel submerged in gas at temperature T. Molecules constantly collide with the paddles, jiggling the system in all directions. At first glance, it seems the ratchet should only allow forward rotation, harnessing these random collisions to do work, as if it could lift a weight using nothing but heat from the bath.

If this were possible, it would blatantly violate the second law of thermodynamics, which prohibits the extraction of net work from a single heat reservoir in a cyclic process. However, Feynman’s deep analysis showed that the ratchet and pawl, when both are at the same temperature, will not rotate preferentially—it just jitters back and forth. The pawl itself is subject to Brownian motion, occasionally bouncing up and letting the ratchet slip backwards. Over time, the number of forward and backward steps equalizes, so no useful work is extracted.

When Does the Ratchet and Pawl Become a Heat Engine?

The twist comes when you introduce a temperature difference. If the paddles are hotter than the ratchet and pawl, the pawl is less likely to bounce, so the device can turn in its designed direction, lifting a weight—essentially functioning as a heat engine. Conversely, if the pawl is hotter, it will occasionally let the gear slip backward, possibly causing net reverse motion. In both cases, energy is extracted from the temperature difference—not from perpetual motion or a violation of thermodynamic law.

Feynman’s analysis mathematically captured these probabilities: the chance of the pawl lifting over a tooth (for backward movement) and the probability of the vanes gathering enough energy to push the ratchet forward are both dictated by the Boltzmann factor (e^{-ε/kT}). When T1 ≠ T2, a net rate difference appears, producing measurable work. When T1 = T2, everything balances and no net motion occurs.

Key Thermodynamic Implications

• No machine, no matter how cleverly designed, can extract net work from a single heat bath in a cyclic process. This is a direct consequence of the second law of thermodynamics.
• Irreversibility in the ratchet and pawl arises not from the device itself but from the statistical probabilities of microscopic motion, and only when there’s a heat gradient between system parts does work become possible.
• Even complex mechanical setups are bound by the same deep physical laws that govern everything from molecular motion to the evolution of the cosmos.

Order, Disorder, and the Arrow of Time: Entropy and Irreversibility

Feynman’s investigation into the ratchet and pawl is more than mechanics—it serves as a window into the nature of order and disorder. Why do things mix and seldom un-mix? Why do eggs scramble so easily but never unscramble? The answer, woven through the analysis of the ratchet and pawl, is entropy.

Entropy measures disorder—the number of ways a system’s components can be arranged without changing the overall appearance. In a box divided into two sections, one with black molecules and one with white, only a few arrangements count as ‘ordered.’ Remove the barrier, and the molecules mix; now, there are vastly more possible arrangements, i.e., higher entropy. The system naturally transitions from order to disorder, not because the laws of mechanics are irreversible (in fact, they are time-reversible) but because overwhelmingly more configurations are disordered. Thus, the arrow of time, the flow from past to future, emerges from probability and initial conditions, not from a hardwired law.

The ratchet and pawl perfectly exemplifies this principle. Its ‘one way’ behavior only arises in the presence of external order—a temperature difference created, for example, by the sun shining on Earth or cooling processes in machinery. Left isolated, the ratchet wheel would just jitter aimlessly, neither winding nor unwinding, as the relentless march toward maximum entropy dominates all.

Microscopic Origins of Macroscopic Order: More on Reversibility and the Demon’s Paradox

The laws of mechanics, at their fundamental level, don’t distinguish between past and future. For any solution describing a motion, simply reversing time yields another valid solution. So, why do we never see scrambled eggs re-form or gases spontaneously un-mix in real life?

Feynman invoked Maxwell’s Demon, a mythical being (or machine) that supposedly sorts fast and slow molecules to reduce entropy. But realistic designs of such demons, like a spring-loaded trapdoor, are themselves subject to thermal fluctuations, eventually heating up and losing their sorting abilities. The same principle foils any microscopic ‘cheat’ based on ratchets and pawls: their own random Brownian motion guarantees they cannot extract net work at thermal equilibrium.

Thus, irreversibility and the arrow of time are not imposed by the laws of mechanics but emerge statistically, based on starting conditions and the overwhelming likelihood of increasing disorder.

Design Considerations and Technical Nuances

While the fundamental principle is simple, building a robust ratchet and pawl mechanism requires attention to many details. Some of the most important considerations include:

• Pawl Shape and Material: The angle of the engaging edge, material hardness, and spring strength all contribute to reliable locking and minimal wear.
• Backlash Reduction: Adjusting tooth pitch or using staggered multiple pawls can minimize unwanted backward play.
• Contact Forces: If the normal force at the contact point passes outside the centers of the wheel and pawl, the pawl can be forced out of contact under heavy load—unless friction or a secure spring compensates.
• Damping Mechanisms: Elasticity in the pawl or wheel can lead to bouncing, requiring dampers or deadeners to prevent slippage and heating.

Special applications—like those in scientific instruments or safety devices—may require toothless ratchets, high-friction materials, or complex pawl geometries for extra precision and reliability.

Real-World Examples and Specialized Uses

The ratchet and pawl idea has spun off into countless variations and applications in engineering, science, and everyday life.

Hand Tools

Socket wrenches allow users to tighten or loosen nuts and bolts in tight spaces, thanks to the ratchet which lets the handle swing back freely without reversing the bolt.

Grease guns, caulking guns, and cable tensioners all apply similar principles to incrementally dispense or apply force, allowing controlled, non-reversible action.

Lifting and Securing Devices

Cranes, winches, and jacks use ratchets to secure heavy loads so that operators can pause, regrip, or readjust without fear of losing control—especially vital when safety is at stake.

Ratchet tie-down straps and cable ties rely on simple, spring-loaded pawls to cinch and lock, preventing unintentional loosening.

Clocks and Automation

Mechanical clocks and watches use ratchets to keep energy stored—once wound up, the mainspring cannot unwind except through the escapement, ensuring precise timekeeping.

Feed mechanisms, motion counters, and mechanical automation use various intermittent and one-way devices for precise, repeatable, and controlled movements.

Vehicles and Machinery

Bicycle freewheels enable smooth coasting and instant engagement when pedaling resumes. Overrunning clutches serve a similar function in vehicles and industrial automation.

Scientific and Philosophical Devices

The Brownian ratchet (and its conceptual variants) remains a favorite subject in physics classrooms, highlighting the limits of what can (and cannot) be achieved by clever design in the face of fundamental thermodynamic constraints.

Related devices, such as sprag clutches, check valves, and even electrical diodes, illustrate the broader theme of ‘rectification’—allowing action in one direction but not the reverse. However, the same thermodynamic limitations always apply: in thermal equilibrium, even a diode cannot produce useful work from Johnson noise without a temperature gradient.

Beyond the Basics: Biological and Nanotechnological Ratchets

Nature herself exploits ratchet-like principles in molecular motors and cellular machinery. Brownian motors—complex protein structures—extract work from random thermal fluctuations by combining spatial or temporal asymmetry with nonequilibrium conditions (think chemical energy from ATP hydrolysis). These engines are the reason why cells move, muscles contract, and biological processes sustain life, always operating within the laws of thermodynamics.

Modern research continues to explore ratchet principles at the nanoscale, building devices that harness chemical, not just thermal, potentials to achieve directed motion—so long as they respect energy conservation and entropy increase.

Common Pitfalls and Misconceptions

Despite its simplicity, the ratchet and pawl mechanism is often misunderstood. Here are a few points to set the record straight:

• It does not produce perpetual motion; friction, backlash, and thermal effects guarantee that energy loss is inevitable, especially in the absence of external input.
• It cannot ‘cheat’ the laws of thermodynamics. At thermal equilibrium, all one-way mechanisms, whether mechanical, electrical, or otherwise, are stymied by random fluctuations in both directions.
• The appearance of irreversibility is a statistical effect, not a mechanical absolute. With very few particles or over extremely short times, the device may show momentary reversals, but averaged over time, the constraints of physics always win.

Mathematical Analysis: Statistical Considerations and Efficiency Limits

Feynman’s detailed mathematical treatment highlights the limits of the ratchet and pawl as a heat engine, focusing on the interplay of energy, probability, and temperature.

To drive the ratchet forward, enough energy must be pooled to lift the pawl over a tooth (energy ε) and to overcome the load (Lθ). The probability of getting this combined energy from random motion in time τ is given by the Boltzmann factor: (1/τ)exp{-(ε+Lθ)/kT₁}.

Backward motion requires only energy ε, with probability (1/τ)exp{-ε/kT₂}. When both sides are at equal temperature, these rates are balanced and no net rotation occurs. When T₁ > T₂, forward motion dominates; when T₂ > T₁, the system can even run backward!

The ultimate efficiency of the ratchet and pawl mechanism as a heat engine boils down to the Carnot limit: the work extracted from heat flow is always bounded by (T₁ – T₂)/T₁, the theoretical maximum for any reversible heat engine.

Ratchet and Pawl in Modern Research and Technology

The study of ratchet mechanisms is not just academic—modern engineers and scientists are still drawing inspiration from these classic systems.

Brownian motors, synthetic molecular machines, and even proposals for quantum ratchets all draw on the core principle: rectification of random motion (or fluctuations) by means of asymmetry and nonequilibrium conditions. In every case, the same lesson holds: real work only emerges when these asymmetries are coupled to true energy gradients—chemical, electrical, or thermal.

Recent experiments in granular gases have even constructed working ratchet engines, using vibrofluidized beads to mimic molecular chaos and drive small rotors via one-way mechanisms. These experiments confirm, yet again, the impossibility of extracting useful work from equilibrium fluctuations alone.

Frequently Asked Questions About Ratchet and Pawl Systems

Given the prominence and complexity surrounding these mechanisms, many people have questions. Here are answers to some of the most common inquiries:

• Can a ratchet and pawl mechanism create perpetual motion?
  No. The physics of friction and thermal motion guarantee that some energy is always lost, and any attempt to extract work without energy input ultimately fails.
• How does backlash affect performance?
  Backlash is the unavoidable free movement before locking occurs, proportional to the tooth spacing. Multiple pawls or alternative designs can minimize, but never fully eliminate it in practical devices.
• What is the difference between a ratchet and a clutch?
  While both allow one-way motion, clutches may use rolling or friction elements (like rollers or balls) instead of teeth and pawls, sometimes allowing smooth or rapid disengagement and reengagement under specific conditions.
• Why is the mechanism relevant in modern science?
  Ratchet principles underpin not just machinery, but our fundamental understanding of non-equilibrium physics, the emergence of order, and the limits of what machines—and even life—can accomplish.

Summary

From its simple mechanical form to its deep ties with thermodynamics and molecular biology, the ratchet and pawl system stands as an icon of functional ingenuity and scientific insight. By allowing motion in only one direction, it provides security and control in countless tools and devices. At the same time, its analysis by thinkers like Feynman has shown that the universe itself imposes unyielding limits on what can be achieved, tying the directionality of machines to the fundamental flow of time and the inevitable rise of disorder. Whether found in the click of a wrench, the ticking of a watch, or the bustling interior of a living cell, the ratchet and pawl reminds us that behind every turn lies a dance of energy, probability, and natural law.